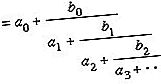ฟังก์ชันซีตาของ Riemannฟังก์ชันมีประโยชน์ในทฤษฎีจำนวนเพื่อตรวจสอบคุณสมบัติของจำนวนเฉพาะ เขียนเป็นζ (x) มันถูกกำหนดไว้ แต่เดิมเป็นseriesζอนันต์ (x) = 1 + 2 -x + 3 -x +4 -x + ⋯ เมื่อ x = 1 ซีรีย์นี้เรียกว่าซีรีย์ฮาร์โมนิกซึ่งเพิ่มขึ้นโดยไม่มีข้อผูกมัดนั่นคือผลรวมของมันจะไม่มีที่สิ้นสุด สำหรับค่าที่มากกว่า x 1 ชุดจะแปลงเป็นจำนวน จำกัด เนื่องจากมีการเพิ่มคำต่อเนื่อง ถ้า x น้อยกว่า 1 ผลรวมจะไม่มีที่สิ้นสุดอีกครั้ง ฟังก์ชันซีตาเป็นที่รู้จักของนักคณิตศาสตร์ชาวสวิส Leonhard Euler ในปี ค.ศ. 1737 แต่เป็นครั้งแรกที่มีการศึกษาอย่างกว้างขวางโดยนักคณิตศาสตร์ชาวเยอรมัน Bernhard Riemann
ใน 1,852 Riemann เผยแพร่กระดาษให้สูตรชัดเจนสำหรับจำนวน primes ถึงวงเงินที่กำหนดไว้ล่วงหน้าใด ๆ - การปรับปรุงตัดสินใจมากกว่าค่าประมาณที่กำหนดโดยทฤษฎีบทจำนวนเฉพาะ. อย่างไรก็ตามสูตรของ Riemann ขึ้นอยู่กับการรู้ค่าที่ฟังก์ชันซีตาในเวอร์ชันทั่วไปเท่ากับศูนย์ (ฟังก์ชันซีตาของ Riemann ถูกกำหนดไว้สำหรับจำนวนเชิงซ้อนทั้งหมด - ตัวเลขของรูปแบบ x + iy โดยที่ i = สแควร์รูทของ√ − 1 — ยกเว้นบรรทัด x = 1) Riemann รู้ว่าฟังก์ชันนั้นเท่ากับศูนย์สำหรับลบทั้งหมดแม้แต่ จำนวนเต็ม −2, −4, −6,
(เรียกอีกอย่างว่า trivial zeros) และมันมีจำนวนศูนย์ในแถบวิกฤติของจำนวนเชิงซ้อนระหว่างบรรทัด x = 0 และ x = 1 และเขาก็รู้ว่าศูนย์ nontrivial ทั้งหมดมีสมมาตรเกี่ยวกับวิกฤต บรรทัด x = 1 / 2 Riemann คาดคะเนว่าศูนย์ nontrivial ทั้งหมดอยู่บนเส้นวิกฤตการคาดเดาที่ต่อมากลายเป็นที่รู้จักในชื่อสมมติฐานของ Riemann
ใน 1,900 นักคณิตศาสตร์ชาวเยอรมัน David Hilbert เรียกว่าสมมติฐาน Riemann หนึ่งในคำถามที่สำคัญที่สุดในคณิตศาสตร์ทั้งหมดตามที่ระบุโดยการรวมอยู่ในรายการที่มีอิทธิพลของเขาจาก 23 ปัญหาไม่แก้ที่เขาท้าทาย mathematicians ศตวรรษที่ 20. ในปี 1915 นักคณิตศาสตร์ชาวอังกฤษก็อดฟรีย์ฮาร์ดี้พิสูจน์ว่าเลขศูนย์มีจำนวนไม่ จำกัด เกิดขึ้นบนเส้นวิกฤตและในปี 1986 ศูนย์รวมที่ไม่เกี่ยวกับสิ่งประดิษฐ์ 1,500,000,001 อันแรกก็แสดงให้เห็นว่าเป็นเส้นวิกฤต แม้ว่าสมมติฐานอาจกลายเป็นเท็จ แต่การตรวจสอบปัญหาที่ยากนี้ได้เพิ่มความเข้าใจในจำนวนเชิงซ้อน