การเรียงสับเปลี่ยนและการรวมวิธีต่าง ๆ ที่อาจเลือกวัตถุจากชุดโดยทั่วไปโดยไม่มีการแทนที่เพื่อสร้างชุดย่อย การเลือกชุดย่อยนี้เรียกว่าการเรียงสับเปลี่ยนเมื่อลำดับการเลือกเป็นปัจจัยชุดค่าผสมเมื่อลำดับไม่ได้เป็นตัวประกอบ โดยการพิจารณาอัตราส่วนของจำนวนชุดย่อยที่ต้องการต่อจำนวนชุดย่อยที่เป็นไปได้ทั้งหมดสำหรับเกมหลายเกมที่มีโอกาสในศตวรรษที่ 17 นักคณิตศาสตร์ชาวฝรั่งเศส Blaise Pascal และ Pierre de Fermat ให้แรงผลักดันในการพัฒนา combinatorics และทฤษฎีความน่าจะเป็น
combinatorics: สัมประสิทธิ์ทวินาม
วัตถุ n ถูกเรียกว่าการเรียงสับเปลี่ยนของสิ่งที่ n นำมาในแต่ละครั้ง จำนวนการเรียงสับเปลี่ยนคือ
แนวคิดและความแตกต่างระหว่างการเรียงสับเปลี่ยนและการรวมกันสามารถแสดงได้โดยการตรวจสอบวิธีที่แตกต่างกันทั้งหมดซึ่งสามารถเลือกวัตถุคู่หนึ่งจากวัตถุที่แยกได้ห้าชนิดเช่นตัวอักษร A, B, C, D และ E หากทั้งคู่ ตัวอักษรที่เลือกและลำดับของการพิจารณานั้นจะพิจารณาผลลัพธ์ 20 ข้อต่อไปนี้:

การเลือกที่แตกต่างกัน 20 แบบที่เป็นไปได้แต่ละแบบนี้เรียกว่าการเรียงสับเปลี่ยน โดยเฉพาะอย่างยิ่งพวกมันถูกเรียกว่าการเรียงสับเปลี่ยนของวัตถุห้าชิ้นที่ถ่ายครั้งละสองชิ้นและจำนวนของการเรียงสับเปลี่ยนที่เป็นไปได้นั้นจะแสดงด้วยสัญลักษณ์5 P 2อ่าน“ 5 permute 2. ” โดยทั่วไปถ้ามี n วัตถุที่มีอยู่จากการที่จะเลือกและพีชคณิต (P) จะต้องเกิดขึ้นโดยใช้ k ของวัตถุที่เวลาจำนวนพีชคณิตที่แตกต่างกันที่เป็นไปได้จะเขียนแทนด้วยสัญลักษณ์n P k สูตรสำหรับการประเมินผลคือn P k = n! / (n - k)! การแสดงออก n! - อ่าน“ n แฟคทอเรียล” - ระบุว่าจำนวนเต็มบวกต่อเนื่องทั้งหมดตั้งแต่ 1 ถึงและรวมถึง n จะถูกคูณด้วยกัน และ 0! ถูกกำหนดให้เท่ากับ 1 ตัวอย่างเช่นการใช้สูตรนี้จำนวนการเรียงลำดับของวัตถุห้าชิ้นที่ถ่ายครั้งละสองรายการคือ

(สำหรับ k = n, n P k = n! ดังนั้นสำหรับ 5 วัตถุมี 5! = 120 การเตรียมการ)
สำหรับชุดค่าผสมวัตถุ k จะถูกเลือกจากชุดของวัตถุ n เพื่อสร้างชุดย่อยโดยไม่ต้องสั่ง การตัดกันตัวอย่างการเปลี่ยนแปลงก่อนหน้านี้กับชุดค่าผสมที่สอดคล้องกันชุดย่อย AB และ BA ไม่ได้เลือกที่แตกต่างกันอีกต่อไป โดยการกำจัดกรณีดังกล่าวยังคงมีเพียง 10 เซตย่อยที่แตกต่างกันเช่น AB, AC, AD, AE, BC, BD, BE, CD, CE, และ DE
จำนวนเซตย่อยดังกล่าวแสดงโดยn C kอ่าน“ n เลือก k.” สำหรับการรวมกันเนื่องจากวัตถุ k มี k! การเตรียมการมี k! การเรียงสับเปลี่ยนที่แยกไม่ออกสำหรับการเลือกวัตถุ k แต่ละตัว ดังนั้นการหารสูตรการเปลี่ยนแปลงโดย k! ให้สูตรการผสมต่อไปนี้:
นี่เป็นเช่นเดียวกับ (n, k) สัมประสิทธิ์ทวินาม (ดูทฤษฎีบททวินาม) ตัวอย่างเช่นจำนวนชุดของวัตถุห้ารายการที่ถ่ายสองครั้ง
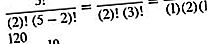
สูตรสำหรับn P kและn C kเรียกว่าสูตรการนับเนื่องจากสามารถใช้เพื่อนับจำนวนการเปลี่ยนลำดับหรือการผสมที่เป็นไปได้ในสถานการณ์ที่กำหนดโดยไม่ต้องแสดงรายการทั้งหมด