ส่วนรูปกรวยเรียกอีกอย่างหนึ่งว่ารูปกรวยในเรขาคณิตเส้นโค้งใด ๆ ที่เกิดจากการตัดของระนาบและกรวยวงกลมด้านขวา ขึ้นอยู่กับมุมของเครื่องบินที่สัมพันธ์กับกรวยการแยกเป็นวงกลมวงรีไฮเปอร์โบลาหรือพาราโบลา กรณีของการตัดกันพิเศษ (เสื่อม) เกิดขึ้นเมื่อระนาบผ่านเฉพาะจุดยอด (สร้างจุดเดียว) หรือผ่านจุดยอดและจุดอีกจุดบนกรวย (สร้างเส้นตรงหนึ่งหรือสองเส้นตรงที่ตัดกัน) ดูรูป
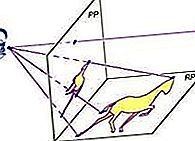
เรขาคณิต projective: ส่วนกรวยที่มีโครง
ส่วนของรูปกรวย s ถือได้ว่าเป็นส่วนระนาบของกรวยวงกลมด้านขวา (ดูรูป) โดยเกี่ยวกับ
คำอธิบายพื้นฐาน แต่ไม่ใช่ชื่อของส่วนรูปกรวยสามารถโยงไปถึง Menaechmus (เฟื่องฟูค. 350 บีซี) นักเรียนของเพลโตและยูด็อกซัสแห่ง Cnidus Apollonius of Perga (c. 262–190 bc) หรือที่รู้จักกันในชื่อ“ Great Geometer” ทำให้ชื่อของพวกเขาเป็นรูปกรวยและเป็นคนแรกในการนิยามสองสาขาของไฮเพอร์โบลา (ซึ่งสันนิษฐานว่ากรวยคู่) บทความแปดเล่มของ Apollonius ในส่วนของ Conic คือ Conics เป็นหนึ่งในผลงานทางวิทยาศาสตร์ที่ยิ่งใหญ่ที่สุดจากโลกยุคโบราณ
คำจำกัดความการวิเคราะห์
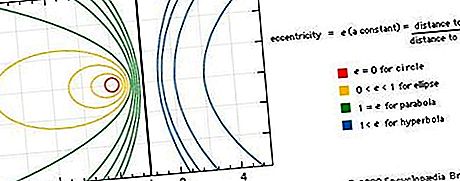
Conics อาจอธิบายได้ว่าเส้นโค้งระนาบที่เป็นเส้นทาง (loci) ของจุดเคลื่อนที่เพื่อให้อัตราส่วนของระยะทางจากจุดคงที่ (จุดโฟกัส) ไปยังระยะห่างจากเส้นคงที่ (the directrix) เป็นค่าคงที่เรียกว่า ความเยื้องศูนย์กลางของเส้นโค้ง หากความเยื้องศูนย์เป็นศูนย์เส้นโค้งจะเป็นวงกลม ถ้าเท่ากับหนึ่งพาราโบลา; ถ้าน้อยกว่าหนึ่งวงรี และถ้ามากกว่าหนึ่งไฮเปอร์โบลา ดูรูป
ทุกส่วนที่เป็นรูปกรวยสอดคล้องกับกราฟของสมการพหุนามระดับสองของรูปแบบ Ax 2 + 2 + 2Cxy + 2Dx + 2Ey + F = 0 โดยที่ x และ y เป็นตัวแปรและ A, B, C, D, E และ F เป็นสัมประสิทธิ์ที่ขึ้นอยู่กับรูปกรวยโดยเฉพาะ ด้วยการเลือกแกนพิกัดที่เหมาะสมสมการของรูปกรวยใด ๆ สามารถลดลงได้หนึ่งในสามรูปแบบ r: x 2 / a 2 + y 2 / b 2 = 1, x 2 / a 2 - y 2 / b 2 = 1 หรือ y 2 = 2px ซึ่งสอดคล้องกับวงรีไฮเพอร์โบลาและพาราโบลาตามลำดับ (วงรีที่ a = b ในความเป็นจริงเป็นวงกลม) การใช้ระบบพิกัดสำหรับการวิเคราะห์เชิงพีชคณิตของเส้นโค้งทางเรขาคณิตที่เกิดขึ้นกับRené Descartes (1596–1650) ดูประวัติของเรขาคณิต: เรขาคณิตคาร์ทีเซียน
ต้นกำเนิดกรีก
ประวัติต้นของส่วนที่เป็นรูปกรวยจะเข้าร่วมกับปัญหาของ "การเพิ่มเป็นสองเท่าของลูกบาศก์" อ้างอิงจากส Eratosthenes ของ Cyrene (ค. 276–190 ก่อนคริสตศักราช) ผู้คนของ Delos ปรึกษา oracle of Apollo เพื่อขอความช่วยเหลือในการสิ้นสุดกาฬโรค (c. 430 bc) และได้รับคำสั่งให้สร้าง Apollo แท่นบูชาใหม่สองเล่มของแท่นบูชาเก่า และมีรูปร่างลูกบาศก์เหมือนกัน งงงวย Delians ปรึกษาเพลโตผู้กล่าวว่า "คำพยากรณ์หมายถึงไม่ใช่ว่าพระเจ้าต้องการแท่นบูชาที่มีขนาดใหญ่เป็นสองเท่า แต่เขาปรารถนาที่จะทำให้งานของพวกเขาน่าละอายชาวกรีกเพราะละเลยคณิตศาสตร์และความดูถูกของพวกเขา สำหรับรูปทรงเรขาคณิต” Hippocrates of Chios (c. 470–410 bc) ค้นพบครั้งแรกว่า "ปัญหา Delian" สามารถลดลงเพื่อหาค่าเฉลี่ยสองสัดส่วนระหว่าง a และ 2a (ปริมาตรของแท่นบูชาที่เกี่ยวข้อง) - นั่นคือการพิจารณา x และ y ที่: x = x: y = y: 2a สิ่งนี้เทียบเท่ากับการแก้สมการสองตัวใด ๆ x 2 = ay, y 2 = 2ax, และ xy = 2a 2ซึ่งสอดคล้องกับสองพาราโบลาและไฮเพอร์โบลาตามลำดับ ต่อมาอาร์คิมีดีส (c. 290–211 bc) แสดงวิธีการใช้ส่วนรูปกรวยเพื่อแบ่งทรงกลมเป็นสองส่วนโดยมีอัตราส่วนที่กำหนด
Diocles (c. 200 bc) แสดงให้เห็นถึงรูปทรงเรขาคณิตที่รังสี - เช่นจากดวงอาทิตย์ - ที่ขนานกับแกนของพาราโบลาของการปฏิวัติ (ผลิตโดยหมุนพาราโบลาเกี่ยวกับแกนสมมาตรของมัน) ที่จุดโฟกัส อาร์คิมีดีสกล่าวกันว่าใช้คุณสมบัตินี้เพื่อจุดเรือข้าศึกติดไฟ คุณสมบัติโฟกัสของวงรีถูกอ้างถึงโดย Anthemius of Tralles ซึ่งเป็นหนึ่งในสถาปนิกของวิหาร Hagia Sophia ในกรุงคอนสแตนติโนเปิล (สร้างเสร็จในโฆษณา 537) เพื่อให้มั่นใจว่าแท่นบูชาสามารถส่องสว่างจากแสงแดดได้ตลอดวัน













